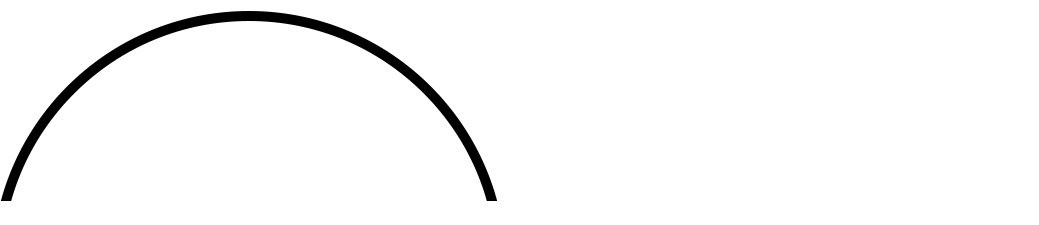POINT-SET TOPOLOGY.

Jul 6

In Ronald Alley’s book Catalogue of the Tate Gallery’s Collection of Modern Art Other Than Works by British Artists, there is a statement from the artist dated the 5th of April 1971, where she describes the series as:

“The unit of the letter ‘U’ or parts thereof are grouped into structures which become part of the whole. . . . POINT AS A SET refers to the language of mathematics, and thus to under-surface relations in nature. . . . My POINT AS A SET series may be considered a continuation rather than a repetition of an idea. Though structurally similar, each work varies in size, configuration, and expression.”

The artist, Claire Falkenstein, was interested in the concept of “point-set topology” in mathematics, also known as “qualitative geometry.” In aligning her work with point-set topology, she explores the nature of shapes and their topological equivalency.

We turned to the paper “Notes on Introductory Point-Set Topology” written by Allen Hatcher, a former professor in the Department of Mathematics at Cornell University in Ithaca, New York. In his paper, Hatcher uses a rubber band to better understand the concept of point-set topology.

If you have a rubber band available, you can follow along or just imagine that there is a rubber band in front of you.

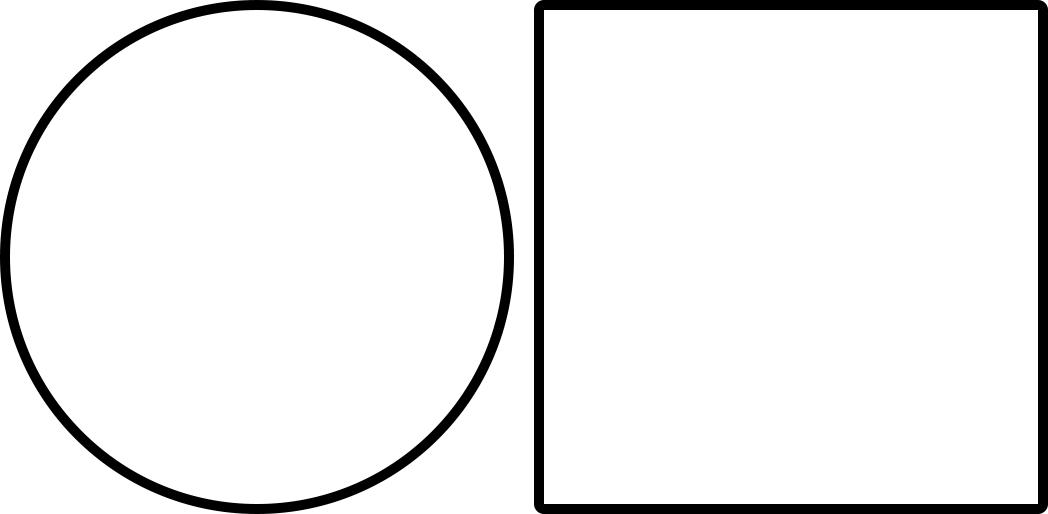
Let’s say that you formed a circle out of this rubber band.

Now shape this circle into a square by pulling on the rubber band to create corners.

A circle and a square are topologically equivalent.

Notice that you didn’t have to break the rubber band to create these 2 shapes.

Now let’s explore a different shape.

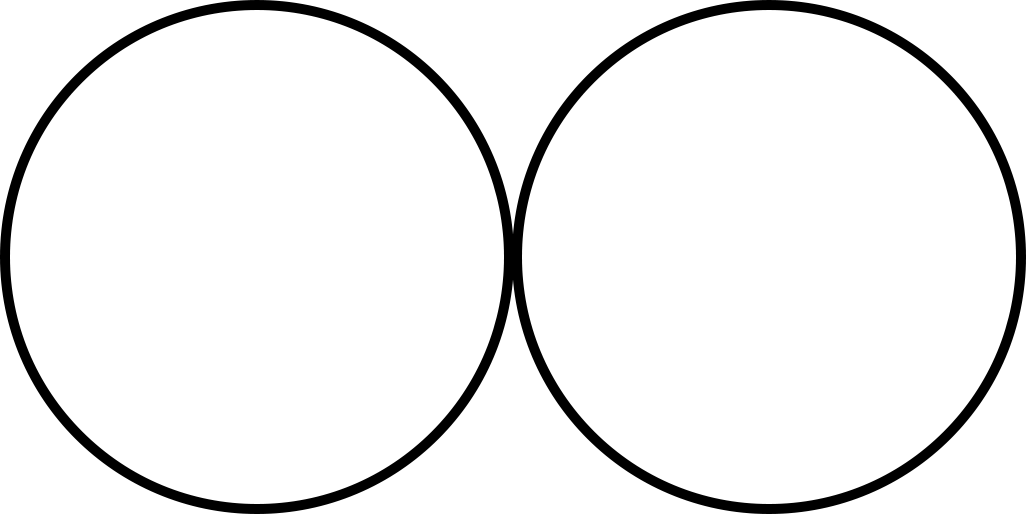
Let’s say that you twisted your rubber band into a figure-8, also known as an infinity symbol, which looks like 2 side-by-side circles that touch at a center point.

A figure-8 is topologically different from a circle and a square.

If you were to remove a point from the figure-8 you would end up with 2 arcs.

When we remove a point from a figure-8, we select the middle of the shape, which is the path of connectedness between the 2 circles.

If you were to remove a point from the circle or square, which are topologically the same, you would get just one arc. This means that a circle and square are topologically different from a figure-8.

When we remove a point from a circle or square, we can do so at any point because the circle has a path of connectedness in the entire shape, as does the square.

Another way to think of topology is referred to as “rubber sheet geometry.” The Encyclopædia Britannica illustrates this concept with a doughnut and a coffee cup.

“Two objects are considered equivalent if they can be continuously deformed into one another through such motions in space as bending, twisting, stretching, and shrinking while disallowing tearing apart or gluing together parts. The main topics of interest in topology are the properties that remain unchanged by such continuous deformations. Topology, while similar to geometry, differs from geometry in that geometrically equivalent objects often share numerically measured quantities, such as lengths or angles, while topologically equivalent objects resemble each other in a more qualitative sense.”

“The main topics of interest in topology are the properties that remain unchanged by such continuous deformations.”

Claire Falkenstein used the U- or arc-shaped copper tubes to create a series of different Point as a Set sculptures. There are 6 different Point as a Set examples below. Notice that the sculptures maintain the same ball shape or topological equivalency, even as the individual ‘U’ copper tubes morph and change, e.g., some tubes are wide, thick, and flat while others are thin, narrow, and round. Some of the Point as a Set sculptures are very dense with a build-up of copper whereas others utilize negative space to create holes and points of entry into the core of the work. Two examples, Point as a Set No. 16 (1965) and Point as a Set (c. 1972) even contain fused and Venetian glass in the center of the ball.